这是一个非常好的问题，我尝试回答一下。

我认为从y到f（x）这是数学思维的升级。

01，代数思维

初中用y，其实还是代数思维——以前我学的初中课本就分为代数和几何。

代数是用字母代替数参与运算，我们从初一就开始学，各种代数式，还有代数式之间的运算……

比如方程，一次的二次的，一元的二元的；还有不等式；复杂的因式分解等。

代数在初中和高中数学中都有很重要的比重。

能用字母参与运算是数学的一项基本能力，这项基本能力在为更高阶的数学做准备。

今后几乎所有的数学运算都在代数式之间展开。

甚至数学定理都是：对于任意的n……

那么在代数式里，y＝9x+6，不是函数，而是代表一个运算结果——如果给x赋值，y就得到一个数。

学二次函数，一次函数的时候也是用y来表示；

函数表达式像一个公式、一个规则；

x经过公式和规则，得到结果y。

事实上初中学生也只能理解到这儿。

在代数系统里，弄一套别的说辞，会晕菜的。

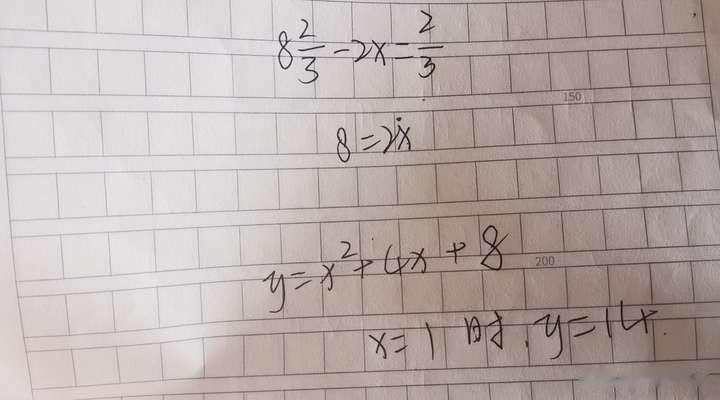
02，关系

数学是抽象的，抽象要缓缓升级。

初中数学的主要目的是配合初中的【九年义务教育】，这是普及性教育，要考虑大多数人的接受程度。

而高中数学带点筛选意味了，抽象要升级，要为后续的高等数学做基础。

所以在这里函数不表示代数计算，而是一种关系——自变量和因变量的关系。

自变量通过一定的【作用function】得到因变量，这个作用就是它们之间的关系——统统叫映射关系，只不过映射关系有很多种，所以有很多函数。

f就是作用，function，x代表定义域——一个集合。

这个集合里的数经过映射关系得到另一个集合（值域）。

高中再用y表示就不合适了，所以用f(x)，更贴近函数本意。

函数既然是关系，就要强调：

自变量和因变量（定义域值域）；

作用——映射关系式；

而函数图像、函数奇偶性、单调性等，属于对某一映射关系观察研究的得出的性质。

很多高中生会背函数的定义，但是并不真正理解。

他们对初中有太强的路径依赖，还觉得函数就是某一种计算。

那么，高考题目中，求定义域、值域、奇偶性、求导等操作，会把他们弄晕的。

毕竟定义都弄不清楚！

他们也理解不了“高考考察的是对基础概念的理解”这句话。

高中数学需要的是思维升级，初中数学计算能力强是刚需，还有勤奋。

维度不同！

03，目的

这样定义其实是为了跟高等数学接轨，从集合论的角度解释函数。

集合论是高等数学的基础，从集合的角度来定义函数，操作函数运算——将来到高等数学部分才不至于迷糊。

有人说，我在高中都迷糊。

高中有很大一部分内容都涉及函数，所以，有句话是“高中得函数者得天下”。

如果说在高中都迷糊，说明不适合学理科——筛选作用，知道自己不擅长。

换个别的路走走呢？

比如学个文科，走对数学要求不那么高的方向。

这不说明你笨，而说明你的天赋在别处。

好，最后推荐一本书，写的通俗易懂。

是讲函数概念的。

这本书是《数学与生活4——函数》。

日本数学家远山启的系列数学科普书《数学与生活》中的其中一本，对于普通人，还有高中生理解函数还是很有帮助的。

感兴趣可以看一看，看过之后就理解【作用】【映射】【定义域】等概念了。